数字签名
作用:保证数据的完整性、不可抵赖性
1、服务器产生公钥和私钥,将公钥给到客户端
2、服务器要发送信息给客户端
3、服务器使用某一hash算法计算这段信息的hash值
4、服务器使用私钥加密hash值,加密后的东西称为数字签名
5、服务器将信息原文和数字签名发送给客户端
6、客户端收到后,使用公钥解密数字签名得到hash值 h1
7、客户端使用相同的hash算法计算收到信息的hash值 h2
8、数字签名解密出来的hash值和自己计算的hash值进行对比,h1 = h2 则说明信息没有被篡改
存在问题
公钥发送过程被攻击者替换的话,攻击者就可以冒充服务器发送信息。
解决方法
通过第三方来保证收到的公钥是属于服务器的
CA证书
CA(证书认证机构)提供服务器身份认证服务,使客户端可以信任被认证的服务器
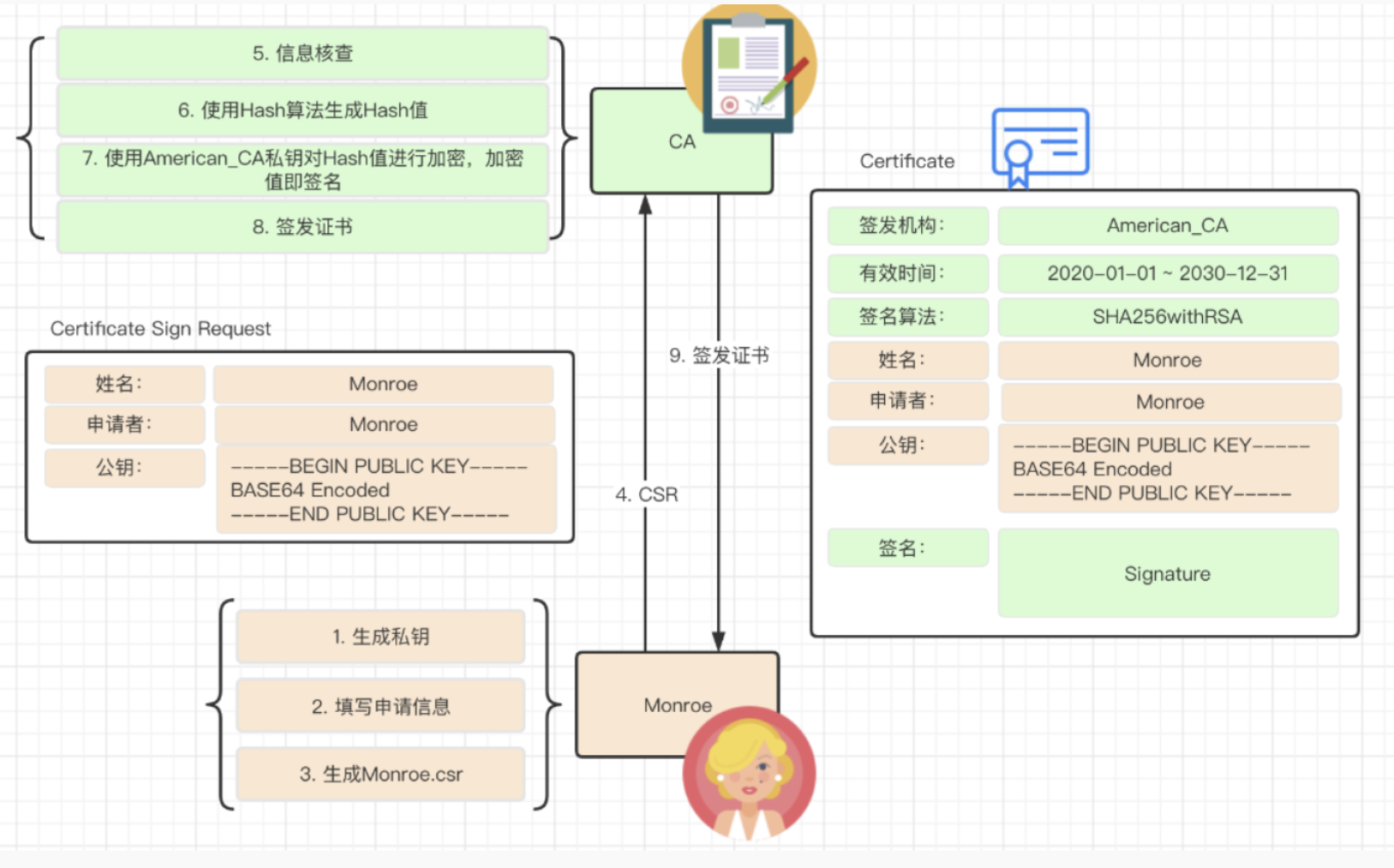
1、服务器生成自己的公私钥
2、服务器向CA发送以下信息:申请者、姓名等服务器详细信息,服务器公钥。称为CSR(Certificate Signing Request)
3、CA生成自己的公私钥,公钥给到客户端(以根证书发放的形式
)
4、CA从线上线下核查认证服务器信息以后,使用hash算法对信息(包括服务器公钥的信息摘要)计算生成hash值,再使用私钥加密hash值,加密后的东西称为CA的数字签名
5、CA使用数字签名签发证书(CA证书),证书上包括 签发机构、hash算法、有效时间、数字签名等重要信息
6、CA证书发给客户端
7、客户端收到证书后,用CA公钥解密数字签名得到hash值 h1
8、客户端自己用hash算法计算csr得到hash值 h2
9、h1 = h2 则说明证书合法,服务器信息真实,服务器公钥真实
存在问题
如何保证CA证书不被伪造?即如何保证客户端的CA公钥是真实的,而不是被攻击者截取替换的?
解决办法
从物理层面杜绝,信息系统默认安装根证书,根证书里面记录了可以信任的CA机构以及其公钥。
https
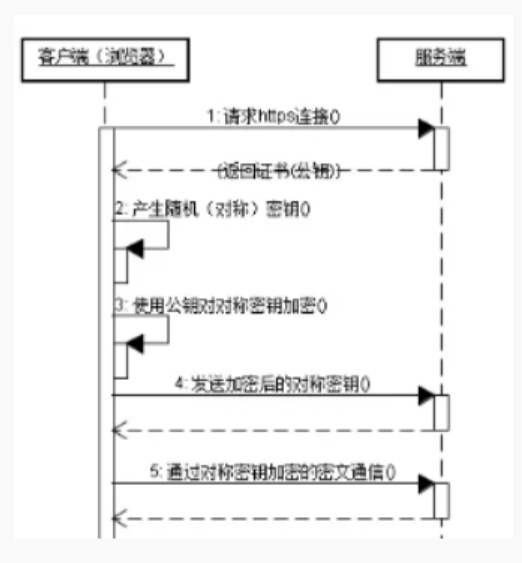
使用对称加密通信的目的是加解密速度较快
SSL使用握手阶段建立安全连接,密钥交换阶段生成对称密钥(此阶段的数据交换使用公私钥加密),然后使用对称密钥进行加密和解密通信数据。这样可以确保通信的机密性、完整性和身份验证。
AES-128
以128位密钥长度来说
1、分组填充,将数据分成128位的数据块,不够128位的填充至128位
2、轮密钥生成,通过加密密钥生成10轮密钥
- 对于128位密钥长度的AES(AES-128),共生成10轮密钥。
- 对于192位密钥长度的AES(AES-192),共生成12轮密钥。
- 对于256位密钥长度的AES(AES-256),共生成14轮密钥。
3、将每组128位数据和128位原始密钥进行异或运算
4、轮函数迭代加密,第一至第九轮包括四个步骤:字节代换、行移位、列混合、轮密钥加,第十轮不包含列混合步骤
- 字节代换通过S盒实现,将一个字节的八位分成两个四位,前四位代表行数,后四位代表列数,将行列锁定的表中的字节替代原来的字节
S盒如下表
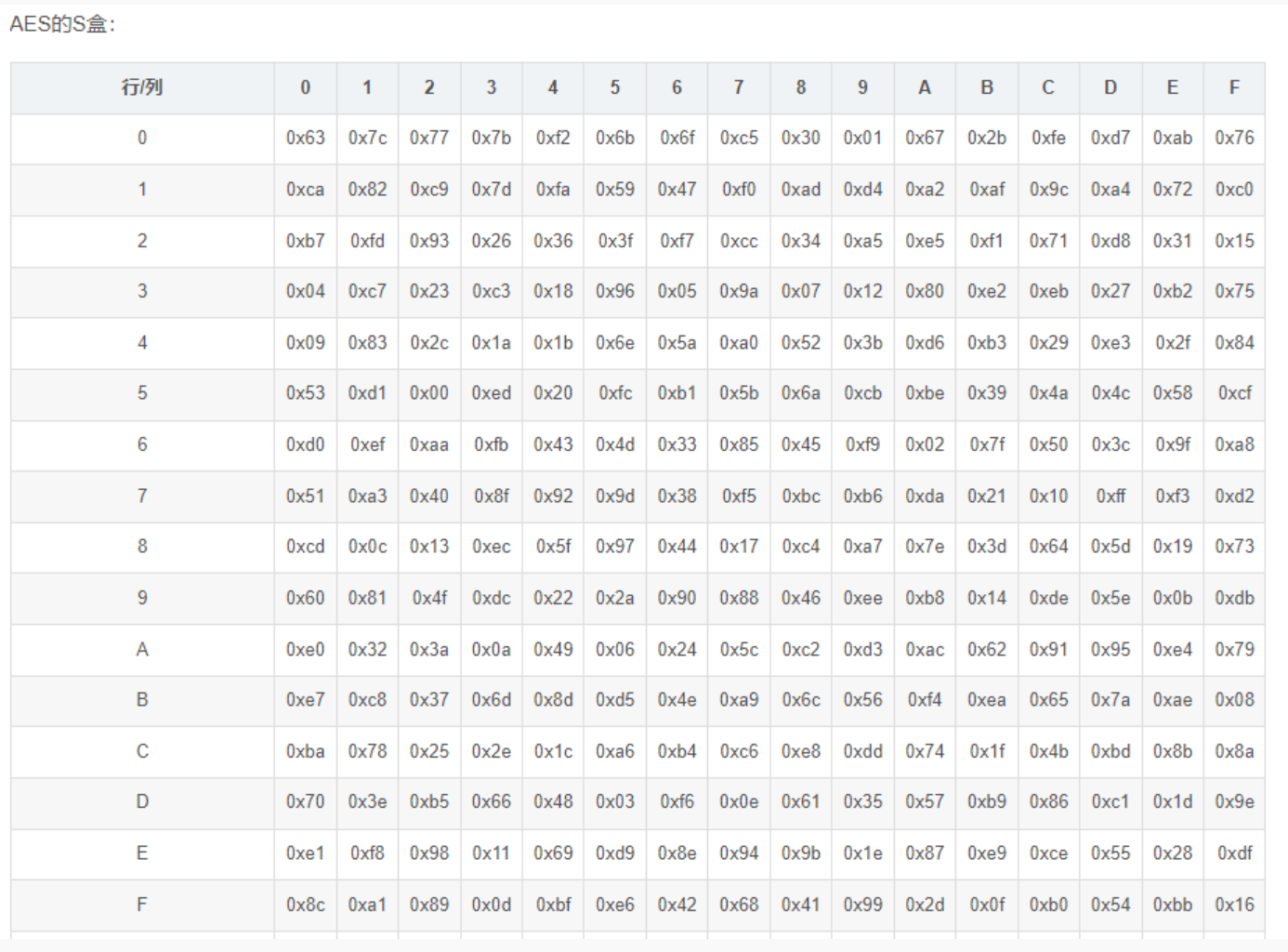
假如原字节是十六进制表示为0x12,二进制表示为00010010的数据,把它分成两段0001和0010,十六进制表示为0x01和0x02。
那么行数为1(0x01),列数为2(0x02)对应的表中数据为0xc9,此时使用0xc9替换0x12,到此就完成了字节替换。
-
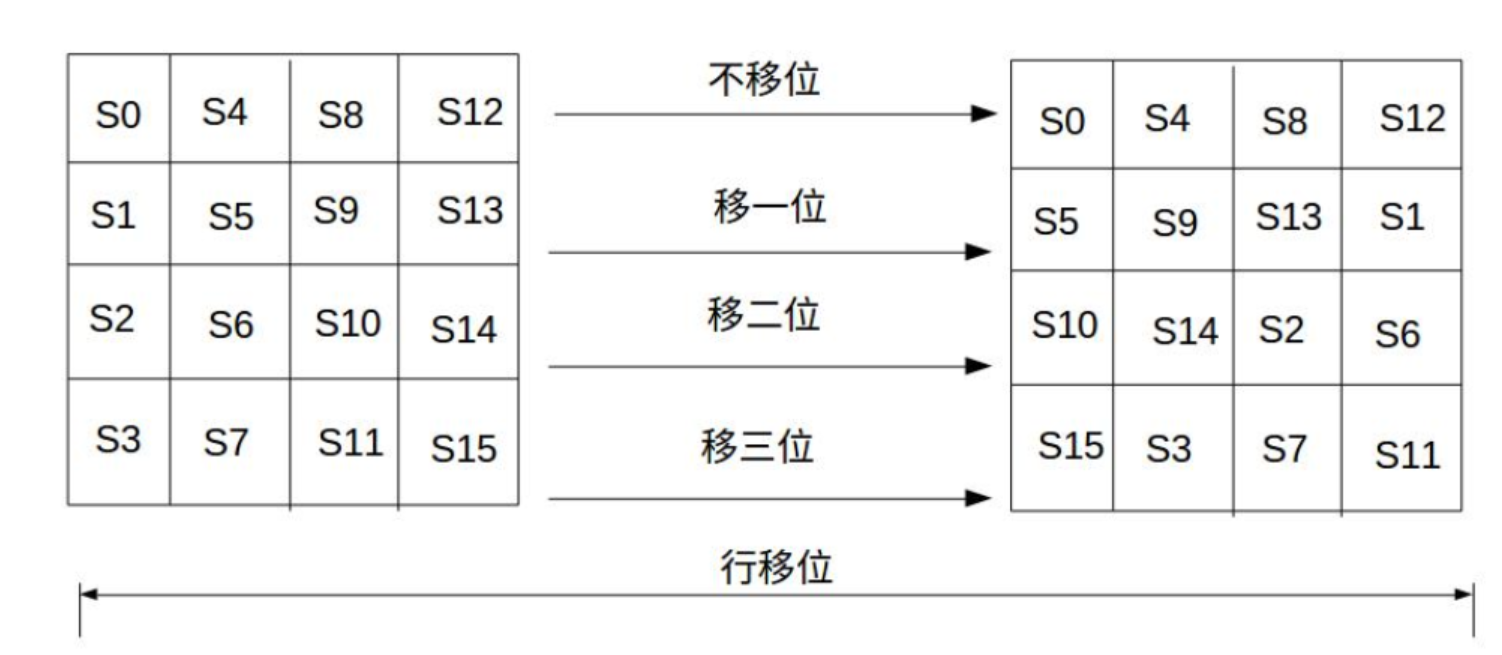
行移位以十六字节状态矩阵为基础,第0行左移0位,第1行左移1位,以此类推。如图:
-
列混合以状态矩阵和特定正变换矩阵相乘实现列混合

-
轮密钥加经过字节代换、行移位、列混合以后的数据和轮密钥数据进行异或运算
5、迭代以后就得到密文
RSA
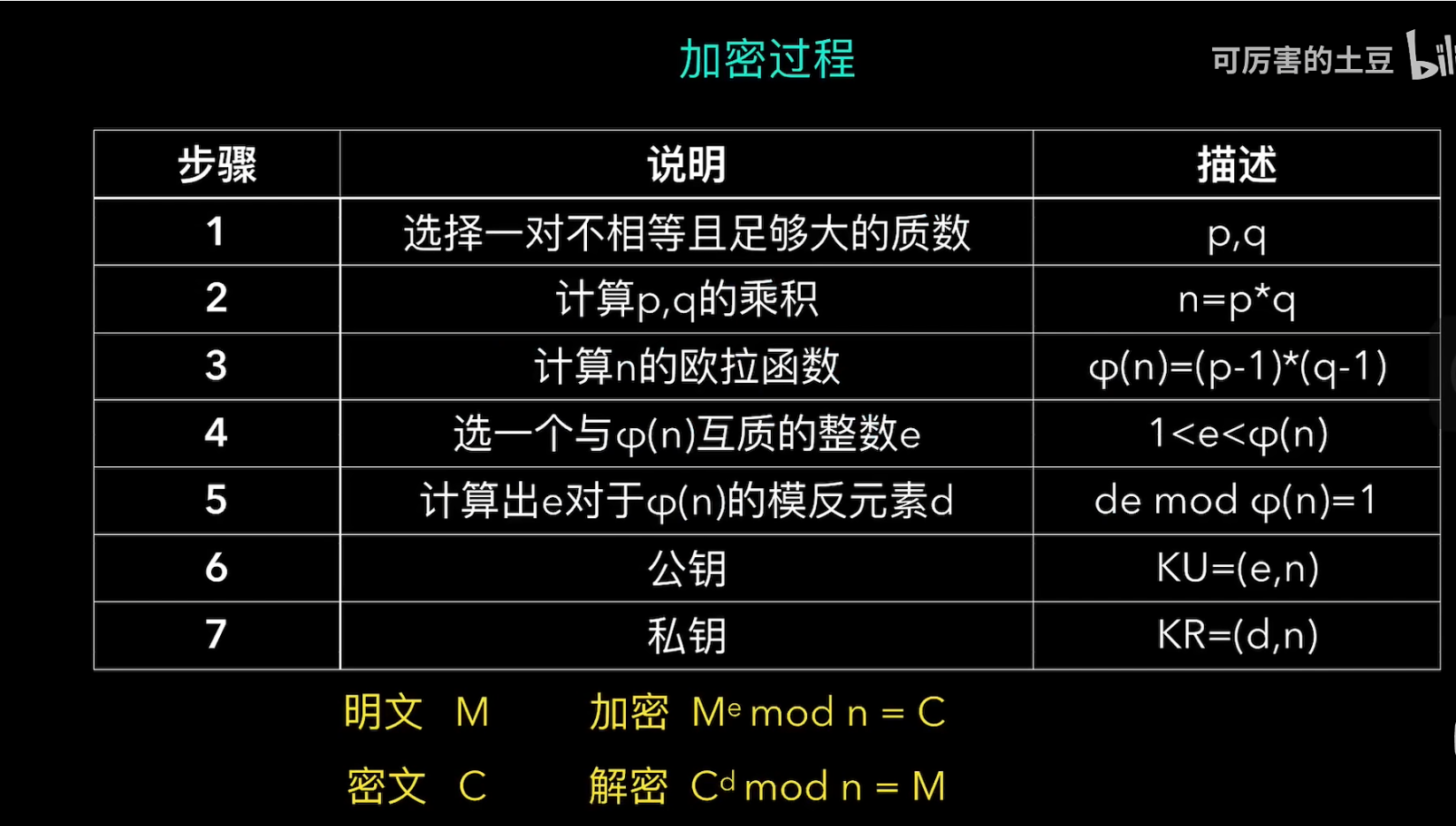
M message
C ciphertext
质数
在大于1的自然数中,除了1和它本身外不再有因数的自然数称为质数。
互质
两个公约数只有1的整数称为互质整数
欧拉函数
ɓ(n)
小于n的整数中与n互质的整数个数
质数的欧拉函数
如果n是质数,它的欧拉函数等于多少
n-1 # 这里减去的1代表它本身,比如n=7,那么小于7与7互质的整数有1,2,3,4,5,6,一共 7-1=6 个。
定理
如果n能分解为两个质数p,q的乘积,那么n的欧拉函数值 等于p的欧拉函数 乘以 q的欧拉函数
结论
如果 n=p*q
那么 ɓ(n) = ɓ(p) ɓ(q) = (p-1) (q-1)
模反元素
如果两个正整数e和ɓ(n)互质,那么一定可以找到一个整数d,使得ed-1被ɓ(n)整除,或者说ed除以ɓ(n)所得余数为1.此时,d就叫做e的模反元素。
*即 ed-1 = k ɓ(n) ,ed-1 是 k倍ɓ(n)**
可写做 ed mod ɓ(n) = 1
也可写做 ed = 1(mod ɓ(n))
模反元素计算举例
假设e=3,ɓ(n)=11,根据上式计算
d=(k*11+1)/3
根据k值的不同,d值也有多种可能
当k=1,可以整除,d=4;
当k=4,可以整除,d=15;
......
至此,公私钥已全部得出
本文作者为A9bot,转载请注明。